4. Les 22 - STEILERE BOCHTEN VLIEGEN
- Tijdens een bocht neemt de belastingsfactor toe, waardoor de overtreksnelheid toeneemt.
MEER HELLING: DAN OOK MEER SNELHEID
Een zweefvliegtuig overtrekt in een bocht eerder dan bij gewoon rechtuitvliegen. Dit komt doordat bij het maken van een bocht de richting van de lift verandert.
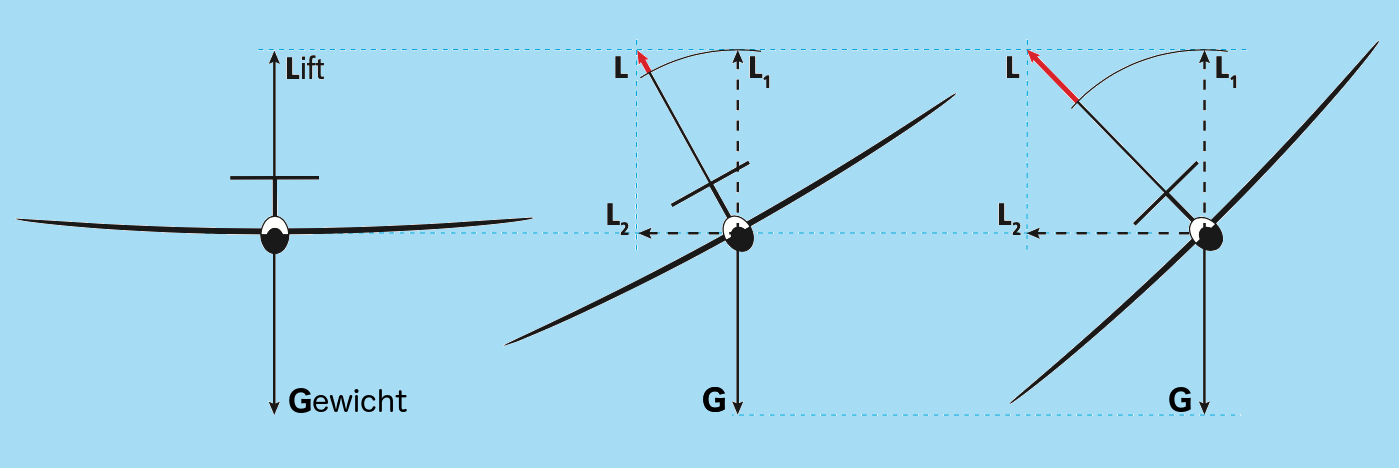
Bij rechtuitvliegen staat de lift recht tegenover het gewicht van het vliegtuig. Bij het vliegen van een bocht staat de lift nog steeds loodrecht op de vleugels, maar door de helling niet meer recht tegenover het gewicht. De lift is te ontbinden in een horizontale en verticale component. L1 is gelijk aan het gewicht van het vliegtuig. L2 geeft de centrifugaalkracht bij het maken van een bocht weer. Hoe steiler we de bocht maken, hoe meer de horizontale component toeneemt. Bij het maken van een bocht neemt de overtreksnelheid toe met de helling.
De belastingsfactor drukt de belasting uit waaraan de structuur van het zweefvliegtuig wordt onderworpen. Je berekent de balastingsfactor door de lift te delen door het gewicht. Wanneer een tweezitter met inzittenden bijvoorbeeld 600 kg weegt en horizontaal vliegt met een lift van 600 kg dan is de belastingsfactor 600 kg/600 kg is 1. We zeggen ook wel de G-kracht is dan 1.
Deze G-kracht neemt toe tijdens bochten. In een bocht met een hellingshoek van 60° is de belastingsfactor 2 g. Met andere woorden: de G-kracht is nu twee keer zo groot als het gewicht van het zweefvliegtuig, en de hoeveelheid lift die dit compenseert is ook twee keer zo groot. Net als in een achtbaan heb je dan het gevoel dat je in je stoel wordt geduwd. Zweefvliegtuigen zijn zeer sterk gebouwd. Ze zijn vaak bestand tegen een positieve belasting van meer dan 5 keer het gewicht van het zweefvliegtuig.
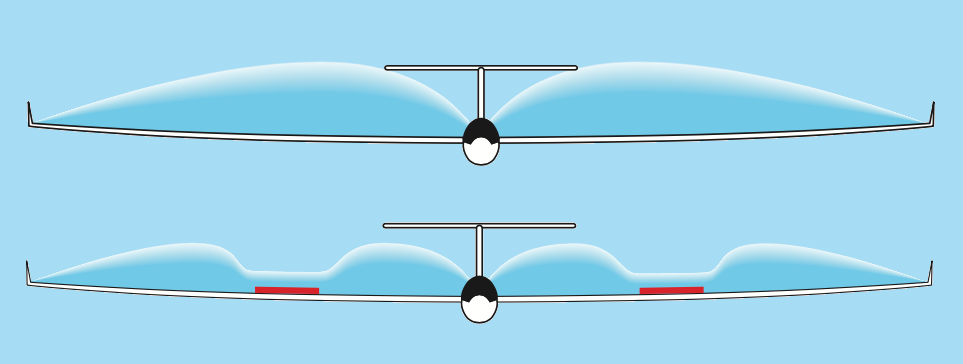
Op de bovenste afbeelding zie je dat de lift gelijkmatig over de vleugel verdeeld is. Als we de remkleppen openen, wordt de lift niet meer gelijkmatig over de vleugels verdeeld. De maximale positieve belastingsfactor is bij veel zweefvliegtuigen dan 3,5 maal het gewicht van het zweefvliegtuig. Bij de remkleppen zal de vleugel eerder breken
Het belangrijkste doel van de remkleppen is natuurlijk dat we veilig kunnen landen. Door extra weerstand te veroorzaken, kunnen we steiler dalen. Maar remkleppen zijn niet erg effectief in het verminderen van de snelheid in een steile duik. Je leert hier meer over in les 4.24 Spiraalduik en tolvlucht.

Tijdens een horizontale vlucht kan 100% van de lift worden gebruikt om het gewicht van het zweefvliegtuig te compenseren. In een bocht met een dwarshelling van 45° is slechts 70% van de lift beschikbaar om het gewicht te compenseren, terwijl de belastingsfactor is toegenomen. Dit betekent dat we tijdens bochten de snelheid moeten verhogen om extra lift te krijgen.
Meer helling: meer snelheid
Vooral bij steilere bochten moeten we er terdege rekening mee houden dat we de snelheid voldoende aanpassen. De draagkracht (lift) neemt in het kwadraat toe met de snelheid (2 x zoveel snelheid is 4 x zoveel lift). Bij het maken van bochten moeten we er rekening mee houden dat de overtreksnelheid met de toenemende dwarshelling ook toeneemt. In het tabelletje wordt de toename van de overtreksnelheid voor verschillende hellingen gegeven.
| Dwarshelling | Belastingsfactor | toename overtreksnelheid | overtreksnelheid |
| 0° | + 1 | 0% | 65 km/h |
| 30 ° | + 1,15 | 7% | 70 km/h |
| 45° | + 1.45 | ± 20% | 78 km/h |
| 60 ° | + 2 | 41% | 92 km/h |
| 70° | + 2.92 | 72% | 112 km/h |
De tabel die hierboven staat is een voorbeeld van een zweefvliegtuig met een overtreksnelheid van 65 km/h bij rechtuit vliegen bij 1g. Bij bochten van 30° hoef je de vliegsnelheid maar een beetje te verhogen. Bij steilere bochten verhoog je duidelijk de snelheid. Je doet dat door de snelheid vanuit de normale bocht te laten toenemen.