5.1.2 DE LIFTFORMULE
Hiervoor is beschreven dat de draagkracht afhankelijk is van:
| 1. de luchtsnelheid | (V) | |
| 2. de grootte van het vleugeloppervlak | (S) | |
|
3. de invalshoek van de vleugel 4. de eigenschappen van het vleugelprofiel |
(α) | }CL |
| 5. de luchtdichtheid | (ρ) |
De draagkracht wordt in formulevorm als volgt geschreven: L = CL ½ ρV2 S
De luchtdichtheid geven we aan met het teken ρ en we spreken dit uit met rho. De andere letters betekenen:
| L = | lift, draagkracht in Newton |
| CL = | liftcoëfficiënt (coëfficiënt is de vermenigvuldigingsfactor) De grootte van de liftcoëfficiënt is afhankelijk van de invalshoek en de eigenschappen van het vleugelprofiel. |
| ½ ρ = | Rho (ρ) is de luchtdichtheid in kg/m3 |
| V2 = | de snelheid in m/s van de aanstromende lucht in het kwadraat |
| S = | het vleugeloppervlak in m2 |
We zeggen dan: de lift is gelijk aan de liftcoëfficiënt keer half rho, keer de luchtsnelheid in het kwadraat, keer het vleugeloppervlak.
Eerste voorbeeld:
Een LS4 met 80km/h, 90 km/h en 110 km/h
LS4a plus vlieger = 350 kg = 3500 N
vleugeloppervlak = 10,5 m2
snelheid 80 km/h = 22 m/s
luchtdichtheid = 1,225 kg/m3
L = G (we gaan er van uit dat de lift gelijk is aan het gewicht)
L = CL½ ρV2S dus 3500 = CL * 1/2 * 1,225 * 484 * 10.5 dus CL = 1,1
LS4a plus vlieger = 350 kg = 3500 N
vleugeloppervlak = 10,5 m2
snelheid 90 km/h = 25 m/s
luchtdichtheid = 1.225 kg/m3
L = CL½ ρV2S dus 3500 = CL * 1/2 * 1,225 * 625 * 10.5 dus CL = 0,9
LS4a plus vlieger = 350 kg = 3500 N
vleugeloppervlak = 10,5 m2
snelheid 110 km/h = 30,6 m/s
luchtdichtheid = 1,225 kg/m3
L = CL½ ρV2S dus 3500 = CL * 1/2 * 1,225 *934 * 10.5 dus Cl = 0.6
.jpg)
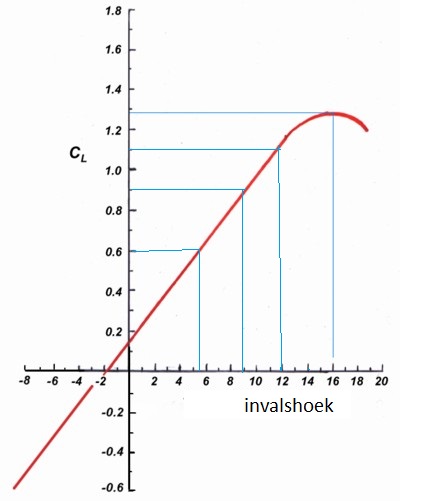
Wanneer je de Cl-waarde hebt uitgerekend, dan kun je in deze grafiek aflezen hoe groot de invalshoek is.
- Bij 80 km/h (Cl = 1,1) vliegt het zweefvliegtuig met een invalshoek van 12° en zit het niet ver van z'n overtreksnelheid.
- Bij 90 km/h (Cl= 0,9) vliegt het vliegtuig met een invalshoek van ongeveer 9 graden
- Bij 110 km/h (Cl= 0,6) vliegt de LS4 met een invalshoek van ongeveer 5 graden.
Tweede voorbeeld:
ASK21 plus 2 vliegers = 600 kg = 6000 N
vleugeloppervlak = 17,95 m2
snelheid 80 km/h = 22.2 m/s
luchtdichtheid = 1,225
L = CL½ ρV2S dus 6000 = Cl * 1/2 * 1.225 * 493 * 17,95 dus Cl = 1,1
ASK21 plus 2 vliegers = 600 kg = 6000 N
vleugeloppervlak = 17,95 m2
snelheid 90 km/h = 25 m/s
luchtdichtheid = 1,225
L = CL½ ρV2S dus 6000 = Cl * 1/2 * 1,225 * 625 * 17,95 dus Cl = 0,9
ASK21 plus 2 vliegers = 600 kg = 6000 N
vleugeloppervlak = 17,95 m2
snelheid 110 km/h = 30.6 m/s
luchtdichtheid = 1.22
L = CL½ ρV2S dus 6000 = Cl * 1/2 * 1,225 * 936 * 17,95 dus Cl = 0,6
Conclusie:
- De snelheid waarmee je vliegt is van grote invloed op de invalshoek en op de draagkracht.
- Met het hoogteroer bepaal je de invalshoek en dus de snelheid.
- De naam hoogteroer klopt eigenlijk niet want het hoogteroer is geen hoogtebesturing (het heet alleen maar zo), maar een "invalshoekbesturing". Als je de invalshoek met het hoogteroer verandert, leidt dit tot een andere liftcoëfficiënt. Als de liftcoëfficiënt verandert, dan moet de snelheid veranderen volgens de liftformule, want het gewicht, de vleugeloppervlak en de luchtdichtheid (op die hoogte) blijven immers hetzelfde.

