7.2.2 REISSNELHEID

Bij grote overlandvluchten is het belangrijk dat je, zodra de thermiek dat toelaat, tempo maakt. Je moet de reissnelheid zo groot mogelijk maken om, voordat de thermiek ophoudt, 'thuis' te komen. Bij goede thermiek kun je, tussen de bellen die je gebruikt om te stijgen, sneller vliegen dan de snelheid voor de beste glijhoek (de snelheid die de MacCreadyring aangeeft wanneer hij op nul staat). Door de MC-ring hoger te zetten steek je sneller. Tijdens het steken verlies je meer hoogte dan nodig is, maar sneller vliegen kan tijdwinst opleveren. Zolang de tijdwinst door sneller te vliegen opweegt tegen de extra tijd, nodig om die extra verloren hoogte weer goed te maken, zit je goed. De som van de tijd om te steken plus de tijd om te klimmen neemt dan af. Vlieg je te snel dan verlies je erg veel hoogte en de totale som van de tijd om te klimmen en de tijd om te steken neemt weer toe.

Hieronder zie je een tabel van een LS4 zonder water (32.2 kg/m²) en tabel van een LS4 met water (45 kg/m²). Beide vliegtuigen laten we een steek maken van 18 km met verschillende snelheden. Eerst klimmen ze beide in een bel van 1 m/s en daarna laten we ze klimmen in een bel van 2 m/s. Bestudeer de tabellen en probeer conclusies te trekken. Wat zijn goede steeksnelheden bij een bel met 1 m/s, bij 2 m/s? Wat is de invloed van waterballast?

De afkortingen betekenen:

LS4 zonder water (32.2 kg/m²)

LS4 met water (45 kg/m²)

1. Je ziet dat de stijgsnelheid in de bel voor de totale tijd het belangrijkst is.
2. Het vliegen met een te grote of een te kleine steeksnelheid levert enig tijdverlies op, maar het vliegen met de MC-ring op 0 m/s levert een groot tijdverlies op (dat is sterk af te raden).
3. In deze situatie is waterballast nuttig. Het levert een hogere reissnelheid op dan zonder waterballast.

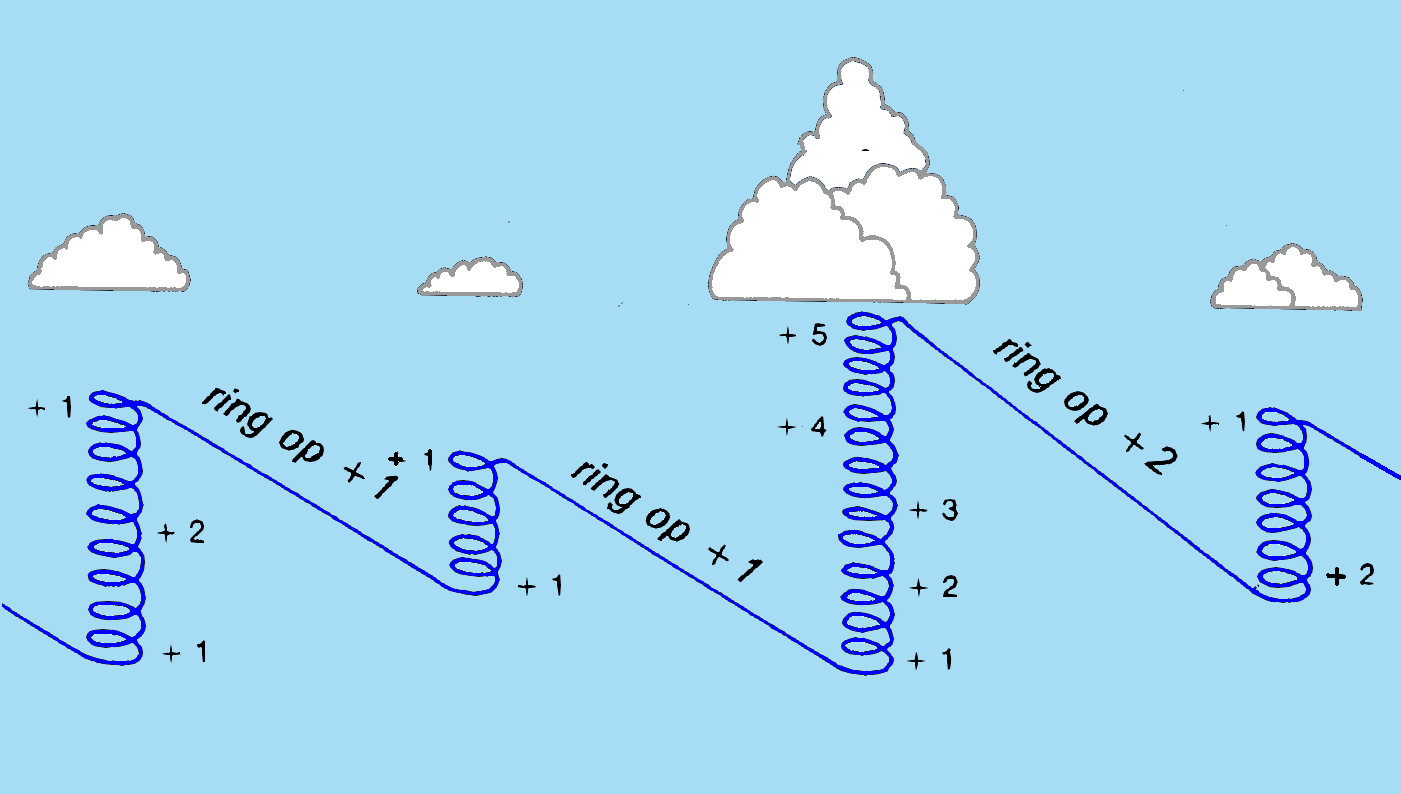
De optimale steeksnelheden blijken overeen te komen met de steeksnelheden die je krijgt als je de MC-ring bij een bel van 1 m/s op +1 m/s zet en bij een twee-meterbel op +2 m/s. Op de volgende afbeelding zie je twee zweefvliegtuigen van het type LS4 zonder waterballast. Ze maken beide een steek van 28,7 km. A vliegt met de MC-ring op 0 m/s en komt na 18 minuten het hoogst in de bel aan. Beide vliegtuigen stijgen in de bel even snel (2 m/s). B vliegt met de optimale MC-instelling en komt 220 meter lager en 6 minuten eerder aan. Na 19 minuten vliegen vanaf wolk 1 komt B in de buurt van de wolkenbasis van wolk 2 aan. Hij heeft dan 4 minuten voorsprong op A. Met de optimale MC-instelling bereik je dus een hogere reissnelheid. Ook hier blijkt weer dat je niet met de MC-ring op 0 m/s moet vliegen.

Twee LS4’s maken een steek van 28,7 km naar een bel van 2 m/s stijgen. Vlieger A vliegt met de MC –ring op 0 m/s en komt na 18 minuten vliegen het hoogst aan. Vlieger B heeft de MacCreadyring op 2 m/s staan en komt na 12 minuten aan, maar wel 220 m lager. Vlieger B heeft bij de wolkenbasis van wolk 2 zo’n 4 minuten voorsprong op A.

In de praktijk maak je nooit een steek van 28 km in rustige lucht naar een bel die op elke hoogte 2 m/s stijgen geeft. Het voorbeeld dient hier alleen om te laten zien wat het voordeel is van vliegen met de optimale MacCready-instelling.

Hoe bepaal je de optimale MC-instelling?

In het voorbeeld wordt er vanuit gegaan dat je van te voren weet dat de volgende bel 2 m/s stijgen geeft, dat het stijgen in de hele bel constant is en dat je de bel haalt. Wanneer je nu de tijd van steken plus de tijd voor stijgen optelt en je doet dit met verschillende MC-instellingen dan blijkt dat je bij 2 m/s de snelste tijd krijgt.

Als je het stuk tussen twee wolken oversteekt met de pijl van de MacCreadyring op +2 m/s gedraaid, dan volg je de hogere snelheden die de MacCreadymeter aangeeft om zo'n gebied sneller over te steken. Zet je de MC-ring nog hoger dan 2 m/s dan steek je nog sneller, maar daardoor kom je (in dit voorbeeld) zoveel lager aan dat de som van steken en stijgen groter wordt. In een bel met constante stijgsnelheid (die je zeker kunt halen) is de optimale MC-instelling gelijk aan het stijgen van die bel. Hieruit volgt een eerste conclusie: de optimale MacCreadyinstelling is nooit hoger dan het stijgen dat je in de volgende bel verwacht.

Alleen stijgen in de sterkste bellen
Je reissnelheid is het grootst wanneer je alleen draait in de sterkste bellen en, tussen die bellen in, steekt met de MC-ring op de optimale MC-instelling. Je kiest je route daarbij zo dat je al MacCreadyvliegend door zwakke stijgwindgebieden heen zoveel mogelijk hoogte 'meepikt' en je draait eerst als het stijgen gelijk is aan je MC-instelling.

Draaien op de hoogte waar de bel het sterkste stijgt
In de praktijk blijkt dat het stijgen in een bel niet constant is. Op een bepaalde hoogte is het stijgen het sterkst. In het onderste stuk en soms ook in het bovenste stuk van de bel is het stijgen vaak minder. Het gebied tussen twee hoogtes waar het stijgen het beste is moet je zoveel mogelijk benutten. Dit zou je de werkhoogte kunnen noemen. Deze werkhoogte verschilt van dag tot dag. Het hangt o.a. af van het verschil in temperatuur tussen de droogadiabaat en de toestandskromme op die hoogte. Daar waar het verschil in temperatuur het grootst is, stijgt de bel het snelst. Onder het vliegen kun je een inschatting maken tussen welke hoogtes het grootste stijgen zit. Je zet de MC-ring niet hoger dan het stijgen dat je gemiddeld in de bel hebt. Boven in de bel neemt het stijgen soms weer af. Als je zeker bent dat het stijgen niet meer is wat het eerst was en de volgende bel is gemakkelijk haalbaar, dan steek je verder. Is de volgende bel ver weg dan loont het om zo hoog mogelijk door te stijgen.

Wanneer je denkt dat je de volgende bel op een redelijke hoogte kunt halen, dan stel je de MC-ring in op het stijgen dat je in de bel had en zodra je verwacht, met deze steeksnelheid op een veilige hoogte in de volgende bel aan te komen, steek je over. Een te lage MC-instelling is minder slecht dan een te hoge. Een te hoge MC-instelling geeft soms een behoorlijke reductie van de reissnelheid. Een te lage MC-instelling geeft slechts een geringe reductie van de reissnelheid. Het volgende voorbeeld probeert dit duidelijk te maken.

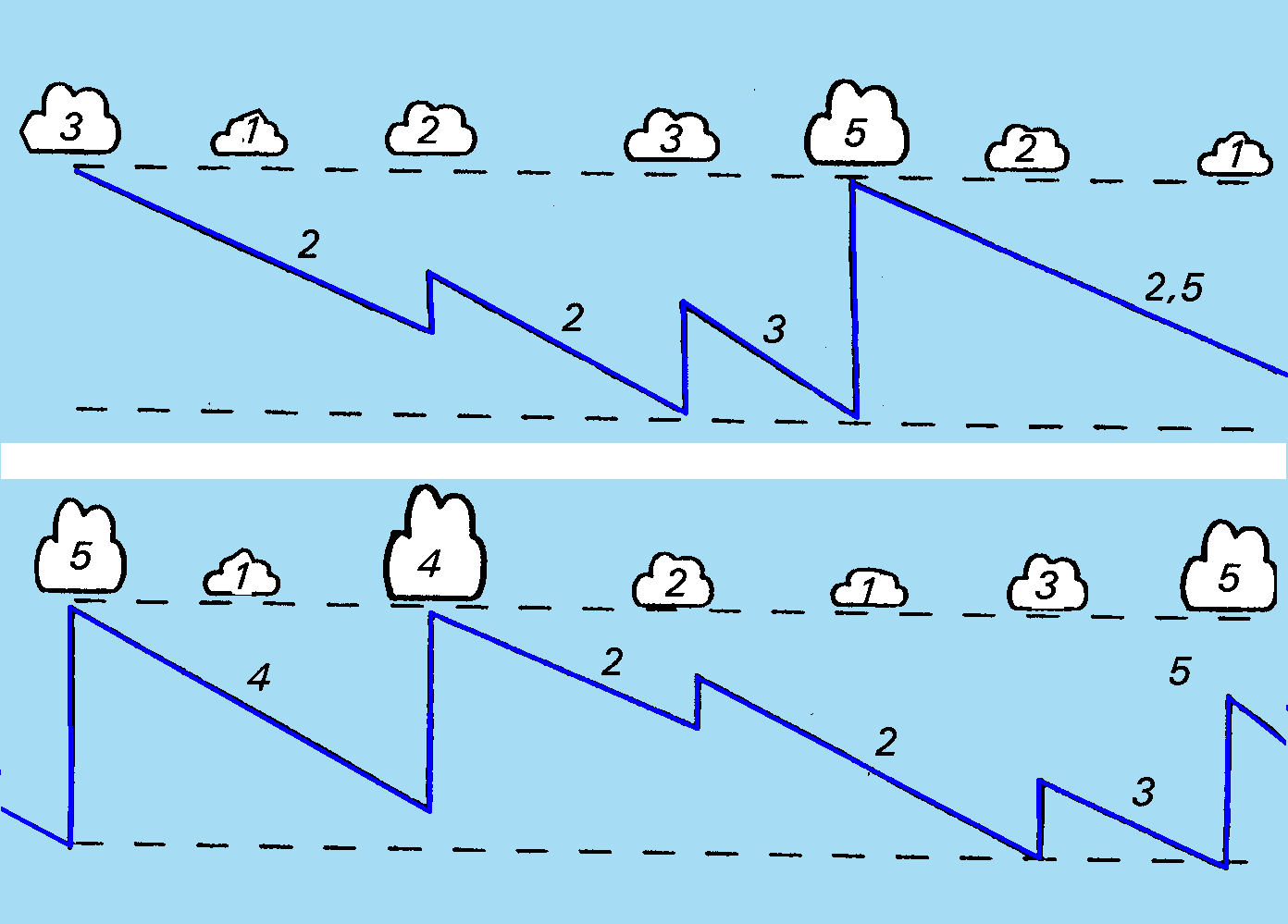
Hier zie je 4 vliegers. Ze maken een lange steek naar een volgende wolk waar ze een grote stijgsnelheid vermoeden. Je ziet hun afstand en hoogte na 25 minuten.

1. Vlieger (1) is voorzichtig, hij stijgt in alle bellen en steekt tussen die bellen met de MCop 0 m/s.
2. Vlieger (2) kiest voor het stijgen dat hij in de volgende bel verwacht en zet de MC = 3 m/s. Hij steekt het snelst en staat meteen aan de grond.
3. Vlieger (3) weet dat hij alleen de sterkste bellen moet pakken. Hij heeft de MC op 0 m/s en slaat het stijgen over; hij steekt langzaam en komt na 25 minuten in de 3 meter bel aan..
4. Vlieger (4) schat dat hij met de MC op 1 m/s op "veilige hoogte" de bel kan halen. Hij slaat het stijgen over en komt na 25 minuten boven in de 3 meter bel aan.

Bij het bepalen van de MacCreadyinstelling houd je rekening met alle bellen, die je 'veilig' kunt bereiken. Als je naar de Veluwethermiek van Terlet vliegt en je zeker weet dat je daar ruim aan kunt komen, klim je niet verder, maar ga je, met de MacCreadyring ingesteld op de stijgsnelheid van de bel die je hebt (of lager), naar die betere thermiek.

In de figuur zie je een deel van een 'optimale overlandvlucht'. Dit geeft je een idee hoe de MacCreadyring ingesteld kan worden. Je ziet dat als de vlieger een goede bel in de verte ziet, hij probeert zo snel mogelijk "op veilige hoogte" bij die bel aan te komen om op die manier zo veel mogelijk gebruik te kunnen maken van het sterkste stijgen dat op een dag door hem gebruikt kan worden. Bij elke steek tussen twee bellen hoort een optimale MC- instelling. Deze is afhankelijk van:

1. het stijgen in de bel waar je in zit
2. het verwachte stijgen onder in de volgende bel
3. de afstand tot de volgende bel
4. het glijgetal van je vliegtuig

Een prestatiezweefvliegtuig kan door zijn hoge glijgetallen veel langere steken maken dan een overgangstrainer. Het is nuttig om deze glijgetallen (bij verschillende snelheden en vleugelbelastingen) te kennen. Je hebt deze kennis nodig bij het bepalen of je de steek naar de volgende bel met de MC-ring op het verwachte stijgen haalt, of dat de afstand te groot is en de MC-ring lager ingesteld moet worden. Bij het berekenen van je final glide heb je dit glijgetal ook nodig. Hieronder zie je een voorbeeld van een MacCreadylijst van een LS4b. In de tabellen met en zonder water zijn voor de verschillende MacCready-instellingen de steeksnelheid, de reissnelheid, de eigen daalsnelheid en het glijgetal weergegeven. Zo'n lijstje kun je in je kniebord meenemen. Het geeft je tijdens de overland in een oogopslag veel nuttige informatie. De afkortingen betekenen:

LS4 ZONDER WATER (32,2 kg/m2)

LS4 MET WATER (45 kg/m2)

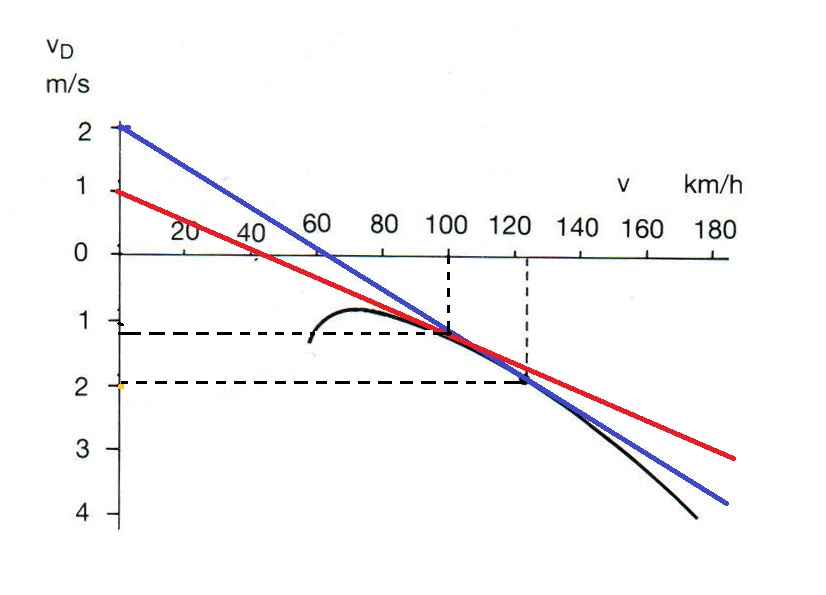
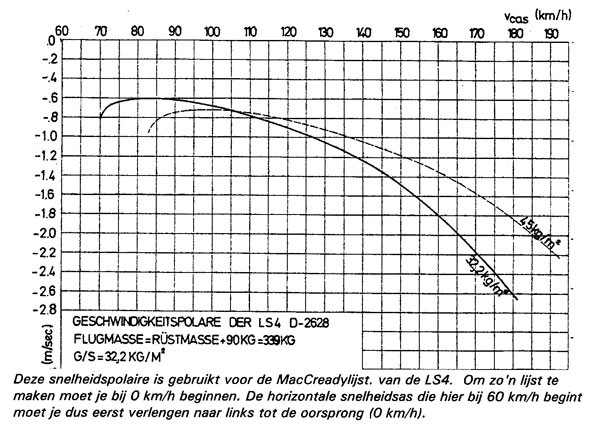
Om voor een zweefvliegtuig zo'n MacCreadytabel te maken heb je de polaire uit het vliegtuighandboek nodig. Op de volgende afbeelding zie je de werkwijze.

Vanuit de MacCready-instellingen (1) en (2) is een raaklijn naar de polaire getrokken. Daar waar de lijn de horizontale snelheidsas snijdt, kun je de reissnelheid aflezen. Het raakpunt met de polaire geeft de steeksnelheid aan en de daarbij behorende daalsnelheid in m/s. In plaats van alle raaklijnen te tekenen kun je ook de lineaal er langs houden.

Glijgetal
Het glijgetal is een heel nuttig gegeven dat je als volgt berekent:V-steek (in m/s) / V-dalen (in m/s) = glijgetal
Je kunt dit glijgetal voor verschillende berekeningen gebruiken:

• Glijgetal gedeeld door 10 = het aantal kilometers dat je met 100 m hoogte kunt afleggen. Stel dat je hoogtemeter op 700 m staat en je hebt bij de huidige steeksnelheid een glijgetal van 30. In rustige lucht kun je dan met een glijgetal van 30 en een hoogte van 700 m dus 7 x 3 = 21 km afleggen.
• Afstand (in m) / glijgetal = de hoogte in meters die je nodig hebt om een afstand af te kunnen leggen. Wanneer je op je kaart of GPS-ontvanger ziet dat je 18 km van je veld zit en volgens deze steeksnelheid heb je een glijgetal van 30, dan heb je in rustige lucht 18000 : 30 = 600 meter hoogte nodig (exclusief reservehoogte).
• Hoogte (in km) x glijgetal = de afstand in kilometers die je kunt afleggen. Staat je hoogte meter op 1200 m en vlieg je met een glijgetal van 33 dan kun je in rustige lucht 1,2 x 33 = 39,6 km afleggen.
• H/1 =1000 / glijgetal = de hoogte in meters die je nodig hebt voor 1 km afstand. Met dit getal kun je snel de benodigde hoogte berekenen. Zit je op 20 km van je veld met de MC-ring op 3 m/s dan heb je 20 x 36 m=720 m hoogte nodig (exclusief reserve hoogte).

Gelukkig beschikken zweefvliegtuigen tegenwoordig over een navigatiecomputer die al het rekenwerk voor ons verricht. Zo'n computer bestaat uit een navigatie display en een elektronische variometer. Het navigatie gedeelte zorgt o.a. voor een snelle aanwijzing van de vliegrichting, de benodigde hoogte om je veld te halen en geeft de verboden gebieden aan. De voordelen van de elektronische vario zijn:

1. Snellere aanwijzing dan een gewone vario.
2. Eenvoudige omschakeling van vario naar sollfahrt
3. Akoestische presentatie. De vario geeft met hoog of laag piepen aan of je goed in de thermiekbel zit. Je hoeft niet steeds op de meter te kijken.
4. Elektronische TE-compensatie.

Bekende merken zijn: LX, Cambridge en Zander. Zo'n computer kan alleen juiste aanwijzingen geven als we van te voren de snelheidspolaire van het type zweefvliegtuig hebben ingevoerd. Verder moeten we nog aangeven of we met water vliegen en of de vleugels schoon zijn.

Regels voor de optimale MacCready-instelling:

• Je komt het snelst vooruit wanneer je de beste bellen eruit zoekt, dat is veel belangrijker dan iets van de optimale MC- instelling afwijken.
• De MC-instelling op 0 m/s houden leidt tot groot tijdverlies, dit moet je dus als het enigszins kan vermijden, als de MC- ring iets te hoog of te laag staat leidt tot gering tijdverlies.
• Het is nooit optimaal om een MC-instelling te kiezen die hoger is dan het stijgen dat je in de volgende wolk verwacht. Sneller steken levert (iets) tijdverlies op, je komt lager aan en onder in de bel is het stijgen meestal minder.
• Het is nooit optimaal om een MC-instelling te kiezen die hoger is dan het stijgen in de huidige bel. Als je de volgende bel op "een veilige hoogte" kunt halen en je vermoedt dat die beter is dan verlaat je de huidige bel op zo'n hoogte dat je kunt oversteken met de MC-instelling op het laatste stijgen. Met "veilig" wordt hier zo'n hoogte bedoeld waarbij je nog aansluiting kunt krijgen. Doorstijgen (met zwak stijgen) tot de wolkenbasis en dan steken met een hogere MC ingesteld op het verwachte stijgen levert geen tijdwinst op.