4.23 SNELHEIDSPOLAIRES ZWEEFVLIEGTUIGEN
| Uitspraak van Jean Renaud, instructeur in La Motte in Frankrijk: "Elke keer wanneer je in een zweefvliegtuig stijgen hebt, dan stort je geld op de bank. Wanneer je aan het steken bent dan moet je zo zuinig mogelijk met je geld omgaan. Niet meer uitgeven dan strikt nodig is. Hoe meer geld je op de bank overhoudt, hoe meer mogelijkheden je hebt. |
Het gaat in dit hoofdstuk over twee dingen
- Tijdens het vliegen in een zweefvliegtuig kom je meer en minder dalende lucht tegen. Bij elke hoeveelheid dalen past bij het gewicht van het vliegtuig een optimale snelheid, waardoor je voor een bepaalde afstand een minimale hoeveelheid hoogte kwijt bent.
- Wanneer je vrij zeker weet dat je een volgende goede bel in de verte kunt halen, dan loont het om sneller te vliegen, dus meer hoogte voor een bepaalde afstand te verbruiken en daardoor eerder bij die stijgende lucht aan te komen.
In moderne zweefvliegtuigen zit een vluchtcomputer die voor jou berekent hoe snel je moet vliegen en hoe hoog je dan op een bepaalde plaats aankomt. Om te begrijpen hoe zo'n computer dat voor je berekent, moet je kennis hebben van de snelheidspolaire.
Snelheidspolaires
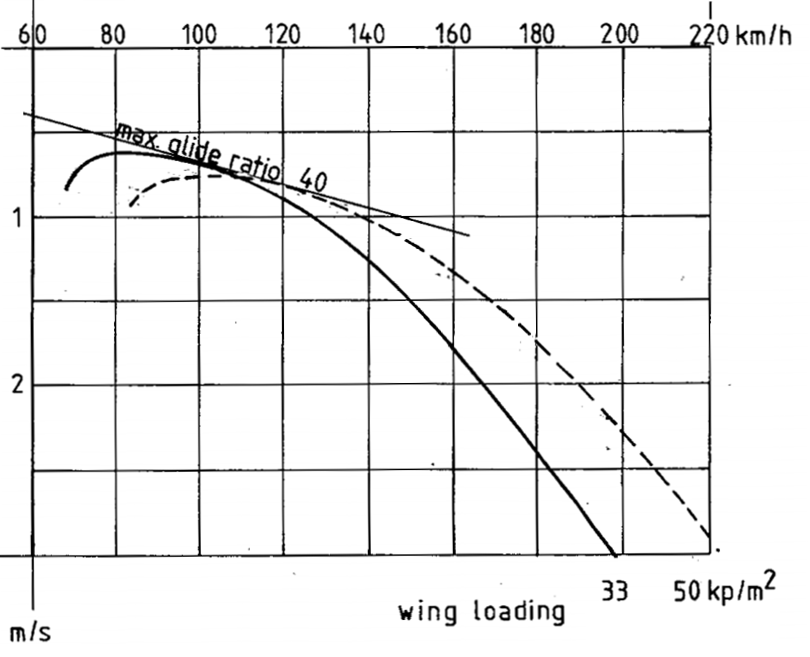
In het handboek van het zweefvliegtuig staat de snelheidspolaire die bij dat zweefvliegtuig hoort. Voor elk zweefvliegtuigtype geldt een andere snelheidspolaire. Hieronder zie je een kopie uit het handboek van een LS4A.
Een snelheidspolaire is een lijn die de hoeveelheid dalen van een schoon zweefvliegtuig in rustige lucht weergeeft bij verschillende snelheden. Je ziet hier twee lijnen. Eén met een vleugelbelasting van 33 kg/m2 en één van 50 kg/m2. Vleugelbelasting wil zeggen het gewicht van het vliegtuig gedeeld door het totale vleugeloppervlak. Een LS4A heeft ongeveer 10 m2 vleugeloppervlak. Bij een vleugelbelasting van 33 kg/m2 heeft dat vliegtuig plus inzittende een gewicht van ongeveer 330 kg. Voor elke vleugelbelasting krijg je zo'n snelheidspolaire.
Voor het bestuderen van de snelheidspolaire moet je de volgende vier punten op de snelheidspolaire kennen:
- Minimum snelheid Dit is de overtreksnelheid. Het vliegtuig begint te schudden en de luchtstroming is niet meer laminair maar begint los te laten en wordt turbulent.
- Minimum daalsnelheid Dit is het bovenste punt op de snelheidspolaire. De daalsnelheid is hier het kleinst. Dit is de beste snelheid om (in rustige lucht) zo lang mogelijk te vliegen.
- Snelheid voor beste glijgetal De snelheid voor het beste glijgetal (beste glijhoek) betekent: de steeksnelheid waarbij met een bepaalde hoogte (in rustige lucht) de grootst mogelijke afstand kan worden afgelegd. In dit punt is de verhouding van daalsnelheid tot vliegsnelheid zo klein mogelijk.
- Maximum toegestane snelheid De maximale toegelaten snelheid is door de fabrikant bepaald aan de hand van sterkteberekeningen van de vleugel.
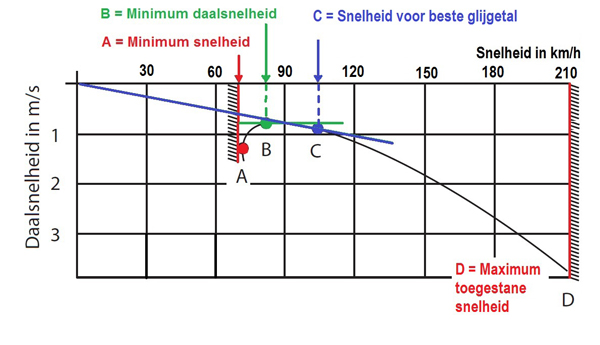
Snelheid voor beste glijgetal
Om de vliegeigenschappen van het zweefvliegtuig waar je mee overland gaat goed te kennen, is het nuttig dat je uit het vliegtuighandboek de snelheidspolaire kopieert en deze bestudeert. Hieronder zie je de snelheidspolaire van de ASW28 met een spanwijdte van 15 meter. Je ziet daarop een polaire met een vleugelbelasting van 31 kg/m2 en een polaire met een vleugelbelasting van 50 kg/m2. Bij een een vleugelbelasting van 31 kg/m2 iis de snelheid voor beste glijgetal 92 km/h en bij een vleugelbelasting van 50 kg/m2 is dat 115 km/h.
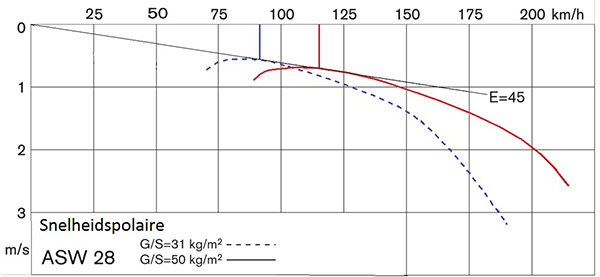
Dit zweefvliegtuig heeft een glijgetal van 45. Met 1 km hoogte kan het zweefvliegtuig 45 km afleggen. De polaire geldt voor een schoon en afgeplakt toestel. Er zijn hier weer twee polaires getekend. Bij een hogere vleugelbelasting schuift de polaire naar rechts en iets naar onderen. De snelheid voor beste glijgetal neemt toe en het dalen neemt iets toe maar het glijgetal blijft gelijk. Bij elke vleugelbelasting hoort een snelheid voor beste glijgetal.
Hieronder tref je de polaire aan zoals je die in het vliegtuighandboek van de DG300 staat.
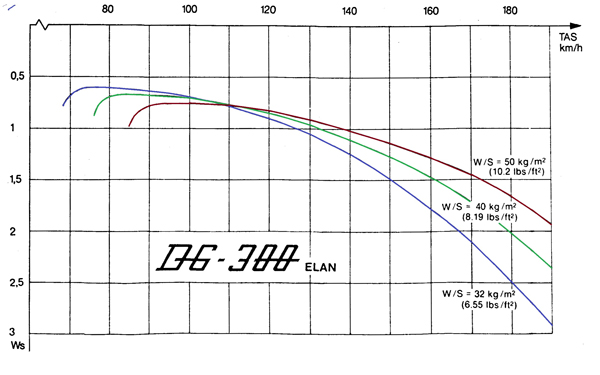
Uit het handboek kun je verder o.a. de volgende gegevens halen:
| Vleugelbelasting W/S | 32 kg/m² | 40 kg/m² | 50 kg/m² |
| overtreksnelheid | 68 km/h | 77 km/h | 86 km/h |
| minimum daalsnelheid | 0,56 m/s | 0,62 m/s | 0,68 m/s |
| bij | 78 km/h | 87 km/h | 98 km/h |
| beste glijgetal | 41 | 41,5 | 42 |
| bij | 100 km/h | 112 km/h | 122 km/h |
- Snelheid en vleugelbelasting Je ziet dat de overtreksnelheid en de snelheden voor minimum dalen en de snelheid voor het beste glijgetal bij een hogere vleugelbelasting hoger geworden zijn.
- Glijgetal en snelheid beste glijgetal Je ziet dat het beste glijgetal bij hogere vleugelbelastingen (vrijwel) gelijk blijft; bij meer gewicht wordt het beste glijgetal bij een hogere snelheid bereikt. Bij de DG-300 wordt bij een hogere vleugelbelasting het glijgetal zelfs nog iets gunstiger. Bij een vliegsnelheid van 122 km/h heb je een daalsnelheid van 0,807 m/s en dan is het glijgetal 42.
Evenwicht van de lift en het gewicht van het zweefvliegtuig
De grootte van de lift is afhankelijk van de vliegsnelheid en van de invalshoek. Bij gewoon rechtuitvliegen zeggen we dat de lift evenwicht maakt met het gewicht van het vliegtuig. Voor een juist begrip van de theorie behoren we te zeggen dat R (de totale luchtkracht) evenwicht maakt met het gewicht van het vliegtuig.
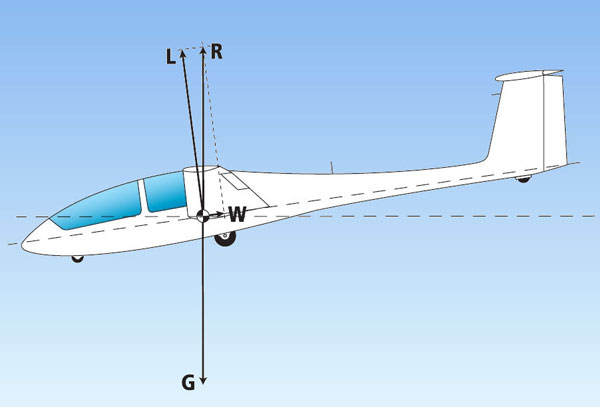
Op de afbeelding zie je dat L (de lift) loodrecht op de luchtstroom staat en G (het gewicht) loodrecht naar beneden wijst. W is de weerstand en die staat precies in het verlengde van de luchtstroom. Recht tegenover het gewicht staat R. R is de resultante, de som van de component lift en de component weerstand. Bij gewoon rechtuitvliegen is L (lift) bijna net zo lang als R. Je kunt in dit geval dus zeggen dat de lift ongeveer gelijk is aan het gewicht van het vliegtuig.
Invalshoek, snelheid en gewicht
Bij de snelheid voor beste glijgetal vlieg je met de meest gunstige verhouding tussen vliegsnelheid en eigen daalsnelheid. Bij de DG-300 (W/S 32 kg/m2.) is dat bij 100 km/h dus 0,67 m/s. Je hebt dan een glijgetal van 41.
Wat gebeurt er als je met de snelheid voor minimum dalen gaat vliegen?Je vermindert de standhoek (neus hoger), dan wordt de invalshoek groter en de snelheid kleiner. Zo ontstaat er weer evenwicht tussen gewicht en lift. Je vliegt dan met de meest gunstige snelheid om zo weinig mogelijk te dalen. Bij de DG-300 (WS 32 kg/m2) is dat bij 78 km/h slechts 0,56 m/s dalen.
Wat gebeurt er als je met en zonder waterballast vliegt en je vliegt bijvoorbeeld in de DG-300 100 km/h?
- Vlieg je zonder waterballast100 km/h in rustige lucht, dan vlieg je met de beste glijhoek (glijgetal 41), dus de gunstigste verhouding tussen vliegsnelheid en daalsnelheid.
- Vlieg je met waterballast100 km/h dan vlieg je met een grotere invalshoek om evenwicht tussen gewicht en lift te bereiken. Je hebt nu niet meer de beste glijhoek (glijgetal 37).
Conclusie: bij elke vleugelbelasting hoort één specifieke snelheid voor minimum dalen en één voor de beste glijhoek.
Bepaling snelheid voor beste glijhoek
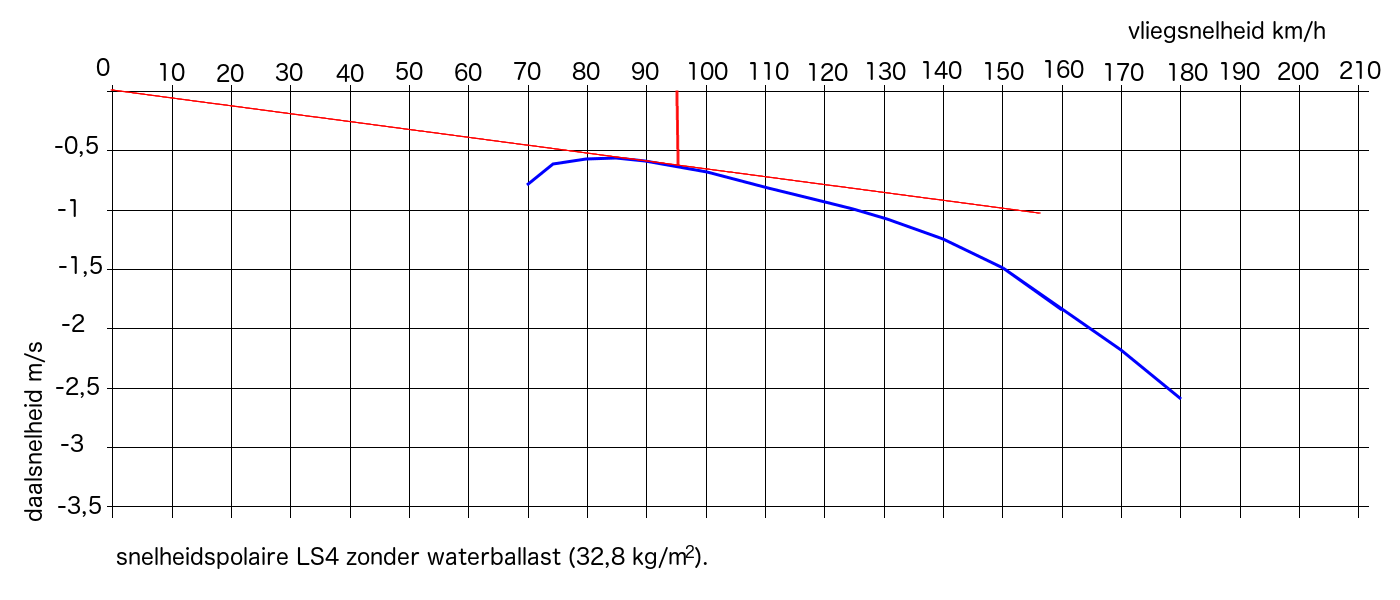
Je bepaalt de snelheid voor het beste glijgetal door vanuit de oorsprong (nulpunt) een raaklijn aan de polaire te trekken. Daar waar de lijn de polaire raakt, trek je een lijn verticaal naar boven om de snelheid af te lezen. Op de afbeelding zie je dat voor een LS4 zonder waterballast die snelheid in rustige lucht ±95 km/h is.
Bepaling snelheid voor beste glijhoek bij vliegen door een daalwindgebied
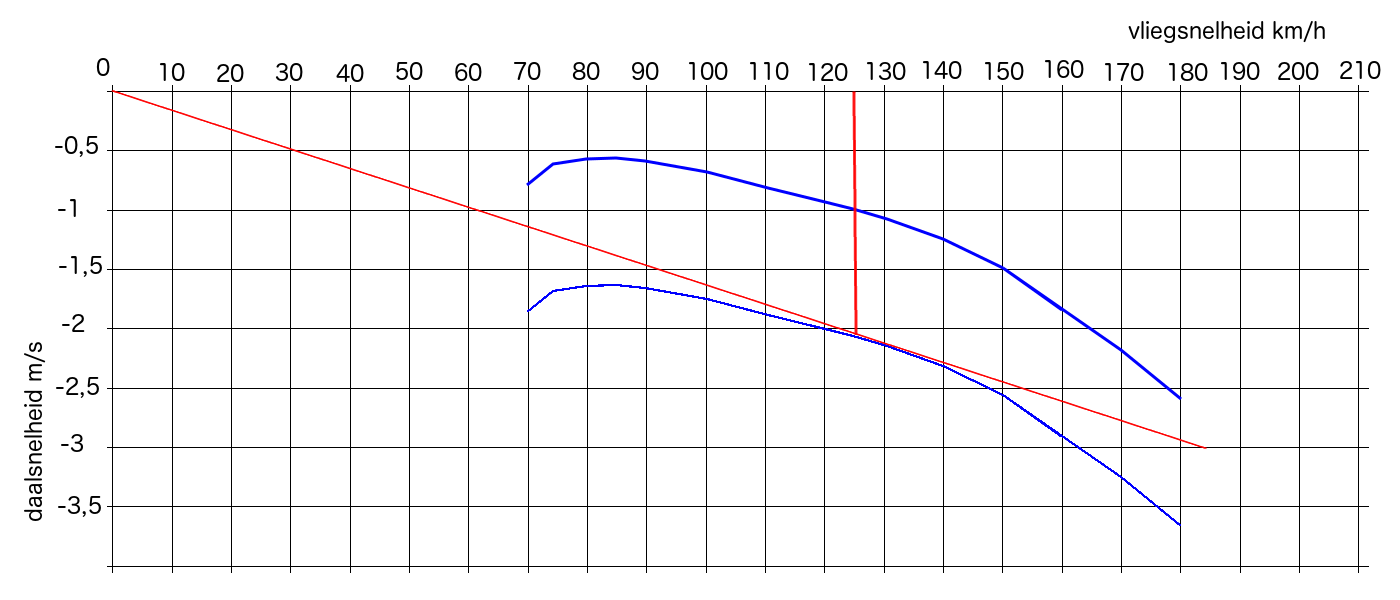
Wanneerje door dalen heen vliegt verschuift de hele polaire naar beneden met de waarde van het dalen. Trek je dan een raaklijn vanuit de oorsprong dan krijg je een hogere snelheid voor de beste glijhoek.
Vlieg je door een daalwindgebied waar de lucht met 1 m/s daalt, dan moet je (in een LS4 32,8 kg/m²) 125 km/h vliegen om de beste glijhoek te krijgen. Zo kun je per vliegtuigtype en vleugelbelasting voor elke hoeveelheid dalen de snelheid voor beste glijhoek bepalen.
Maccreadyring en sollfahrtgeber
Veel zweefvliegtuigen hebben een MacCreadyring om de variometer, een sollfahrtgeber en een final glide computer (of een boordcomputer met o.a een final glide rekendeel). De MC-ring en de sollfahrtgeber zijn bedoeld om zo snel mogelijk afstanden door daal- en stijgwindgebieden af te kunnen leggen of om met de snelheid voor de beste glijhoek terug naar het veld te vliegen. De final glide computer wordt gebruikt om de hoogte en de snelheid te bepalen om optimaal (= zo snel mogelijk) vanuit de laatste bel naar het thuisveld te vliegen.
De MC-ring geeft de beste snelheden om te vliegen zonder waterballast. Bij de sollfahrtgeber (vaak gecombineerd met een akoestische variometer) en de final glide computer is het wel mogelijk de aanwijzingen aan te passen voor verschillende vleugelbelastingen (dus met waterballast). Onthoud dat deze snelheden niet meer kloppen bij een sterk vervuilde vleugel en absoluut niet bij vliegen in de regen. Bij vliegen in de regen houd je ±110 km/h aan en niet de aangewezen MacCreadysnelheden.
Beste snelheid voor daalgebieden
Wanneer je terug vliegt - en er staat niet veel wind - kom je door gebieden waar je dalen hebt en gebieden waar je stijgen ondervindt. Om zo hoog mogelijk (dus niet meer hoogte te verbruiken dan strikt noodzakelijk) bij het veld aan te komen, vlieg je met behulp van de MacCready-ring. Op deze verdraaibare ring, zie je een pijltje (driehoekje). Dit pijltje moet voor dit doel op 0 m/s staan. Voor elk hoeveelheid dalen bij het vliegen door een daalwindgebied wijst de naald van de variometer de vliegsnelheid voor beste glijhoek aan. Deze snelheden volg je globaal. Als de variometer 2,5 m/s dalen aangeeft moet je volgens de hier afgebeelde MC-ring ongeveer 120 km/h gaan vliegen.
Terug vliegen naar je veld tegen de wind in
Wanneer je tegen de wind in zo hoog mogelijk bij je veld of het aanknopingspunt wilt aankomen, dan zul je sneller moeten vliegen dan bij de situatie "geen wind". Hoeveel sneller volgt ook uit de snelheidspolaire. Als je bijvoorbeeld met 35 km/h tegenwind vliegt, trek je niet een raaklijn vanuit het nulpunt maar vanuit 35 km/h op de horizontale as naar de polaire.
Je ziet dat de snelheid die daarbij hoort ±105 km/h is. Wanneer je de raaklijn van 35 km/h naar links doortrekt komt hij voor de LS4 uit op +0,4 m/s. Zet je dus bij 35 km/h tegenwind de pijl van de MC-ring op +0,4 m/s dan geeft hij je de beste glijhoek ten opzichte van de grond waarmee je zo hoog mogelijk bij je veld aankomt.
Onder het vliegen weet je meestal niet precies hoe hard de tegenwind is en daarom schat je de MC-instelling als volgt: bij matige tegenwind de pijl op plus 0,25 m/s en bij krachtige tegenwind de pijl op plus 0,5 m/s.
| tegenwind | sterkte | ringinstelling |
| matig | 5 m/s = 10 knopen = 18 km/h | + 0.25 m/s |
| krachtig | 10 m/s = 20 knopen = 36 km/h | + 0.5 m/s |
| hard | 15 m/s = 30 knopen = 54 km/h | + 0.75 m/s |
Sollfahrtgeber
Een sollfahrtgeber is niets anders dan een elektronische versie van een MC-ring. Ook de sollfahrtgeber geeft de beste snelheid aan om door een daal- of stijgwindgebied te vliegen. Alleen werkt de sollfahrtgeber in de praktijk eenvoudiger. In plaats van de naald van de variometer steeds op de gevlogen snelheid op de ring te houden, houd je nu de naald van de sollfahrtgeber op nul. In plaats van het driehoekje op de ring op bijvoorbeeld plus 1 m/s te draaien, kun je de sollfahrtgeber met de MC-knop instellen op elke stijgsnelheid. Wijst de wijzer hoger aan dan 0 m/s dan vlieg je te snel. Neem snelheid terug en de wijzer van de sollfahrtgeber zal dalen. Wijst de sollfahrtgeber minder dan 0 m/s aan, dan moet je de snelheid verhogen.